4.3. Эллиптические функции Якоби могут быть выражены через тэта-функции: snu-- tnu-V dna-VF

Если положить и для действительных К, К в первый раз взять

Д9900 Д9995 10000-

W 0J9 0,8 0.7 0.6 0 0.4 0.3

ОЯ 0J

о OJ ОЯ 0.3 0.4 0.S- 0£ 0.7 0,8 OS Рис. 79. Величина q:как функция от u*==sin*a.

2К<а <2К,а во второй раз , = 0, то для малых g получим приближенно

1-4o*cos*i/ l-Aq (\-2q) cos*

cna=cosj> (1-Ь2,) 1--4<7(1--2q)smi/

zna:

1 d In

Aq sin 2

ft d ~I-b2g(2-cos2i/)+4qMl-2cos2j)-

XI. ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ

А. ПОЛИНОМЫ ЧЕБЫШЕВА

Полиномы Чебышева 1-го рода Tiz) и 2-го рода U i,z) определяют как*)

7 (г) = cos (л arecos z) = - U (г) = sin (л arccos z) =

{z + iVlzy-i-{z~-iV -zr (z+i yry-iz ~ I yi-zf

Они являются линейно независимыми решениями дифференциального уравнения Имеют место п{)едставления:

Г. И == г -() а-- ) ч-(4) О-..

ЬЗ-5...(2я-1) dz ~

UJz) = V\ -z [( Ч ) z--[ I ) z- (1 -.г) + ( ) z- (l~zr-... =

( !) - 1,3.5 2л 1) dz .:

n- -

П p о и 3 в о Д я 1ц и e фу н к ц и и:

/1=1

Рекуррентные формулы:

Tn+i (2) -22:Т (2) + 7 , (г) = О, , (г) - 22£/ И +1/ , (4 = 0.

Функция (z) обращается в нуль при z = - 1 и z = \. Кроме того, Tf(z) и Uiz) имеют только действительные простые нули, которые все лежат в интервале -1<:2:<;1.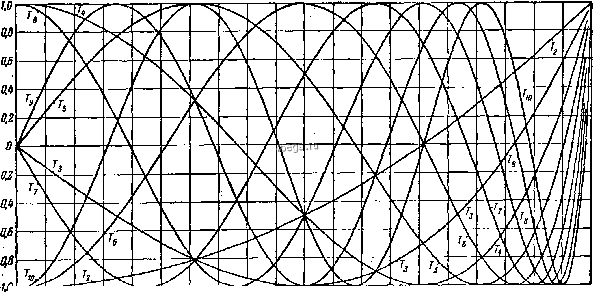

а BLJ 0 0 ол 0.5 Ofi 0.7 Qfi ОД Щ

Рис. 80. Полиномы Чебышева 7я(лс). и==?2, 3, .... Ш.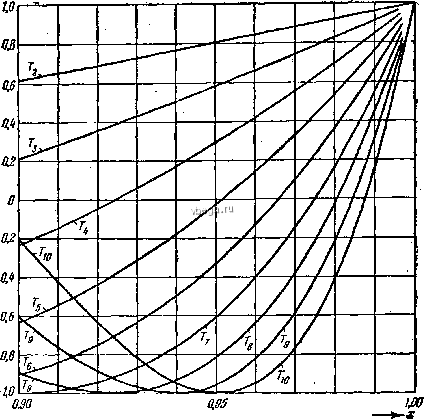

Рис. 81. Полиномы Чебышева Та{х), я=2, 3, .... 10.