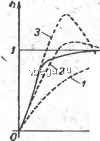создает возрастающая в конце концов колебательность переходного процесса. Применение линейной коррекции позволяет повысить максимально достижимое при этом значение коэффициента передачи, однако принципиально не снимает указанного противоречия, требующего ковшромиссного решения при выборе коэффициента передачи и самой коррекции (см.. седьмую главу). Сказанное иллюстрируется рис. 10-1, где приведены переходные характеристики 1,2, пЗ линейной САУ при трех настройках коррекции, дающих все возрастающую форсировку процесса.

Указанное противоречие можно устранить, если изменять коррекцию в ходе переходного процесса так, чтобы в первой его части коррекция определялась только по условию обеспечения требования к быстродействию, а затем изменялась исходя из требования

к устойчивости и колебательности процесса. При этом коррекция, выбранная для первой части переходного процесса, будет настолько сильной, что если ее не изменять к концу, переходный процесс получится, с очень большой колебательностью вплоть до нвг устойчивости.

Такое изменение коррекции в ходе переходного процесса и, означает переход к нелинейной коррекции, поскольку сводится к изменению структурной схемы или параметров корректи]рун)-щик эвеньев в функции переменных величин, характеризующих процессы в системе. При больших отклонениях от установившегося режима, соответствующих началу переходного процесса, коррекция должна обеспечивать максимально быстрое устранение этого отклонения, а затем, когда отклонение снижено до достаточно малой величины, необходима коррекция, обеспечивающая неколебательное окончание процесса.

Практически такая нелинейная коррекция реализуется либо .с помощью реле, осуществляющего переключение с одного корректирующего звена на другое в функции выходной величины системы или какой-либо другой переменной, либо с помощью нелинейных звеньев со специально подобранной характеристикой, включенных последовательно с линейными корректирующими звеньями и изменяющих коэффициент передачи в ходе переходного процесса. Например, требуемая форсировка при больших отклонениях от уста-ч повившегося состояния может быть получена включением последовательно в примой канал САУ или в каналы форсирующих корректирующих воздействий нелинейного звена с вогнутой характеристикой, подобной приведенной на рис. 10-2. Того же результата можно достигнуть введением нелинейного звена с вы-

Рис. 10-1. Переходная .характеристика системы при нелинейной коррекции.

клой характеристикой типа характеристики с насыщением в цепь рицательной обратной связи или в цепь корректирующих воздействий, демпфирующих переходный процесс.

В результате применения такой нелинейной коррекции может ТВ получен процесс, изображенный на рис. 10-1 сплошной 1лниев. Начальная часть процесса совпадает с переходной харак-Ртеристикой 3 линейной системы, а далее происходит увеличение Гдемпфирввания и процесс переходит в монотонное окончание, подобное концу характеристики 1.

Изложенное показывает большие возможности нелинейной рррекции. В целом, как уже говорилось, нелинейная коррекция одится к применению, во-первых, логиче-корректирующих устройств, изменяю- структуру системы в функции значений переменных и внешних воздействий, и, порих, корректирующих звеньев с нели-йными характеристиками. I. Вмесуа с тем, говоря о достоинствах не-аейррекции, в частности, в линей-сиктемад, следует отметить, что такая коррекция по самой природе является более нзированной по отношению к режимам сийтемы, в которых она дает нужный ект. Может получиться, например, так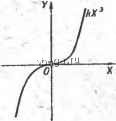

Рйс. 10-2. Статическая характеристика нелинейного корректирующего звена.

ЧТО нелинейная коррекция, выбранная для шределенного вида внешних воздействий, , :ажется не только не эффективной, но даже вредной при других учтенных режимах САУ. Поэтому, чем шире диапазон внешних здействий и вообще условий работыJ;иcтeмы, тем труднее вы-кть нелинейную коррекцию и тем скорее окажется наилучшей Цсе-таки линейная коррекция.

Последнее усугубляется тем, что, к сожалению,не существует ккой-либо общей методики выбора нелинейных корректирующих Хзвеньев, и практически при синтезе приходится прибегать к меоду проб и последовательных приближений, используя опыт и литера- турные рекомендации по применению отдельных частных приемов ;А схем нелинейной коррекции (см. например, [19; 20; 21]).

10-3. ПОРЯДОК СИНТЕЗА НЕЛИНЕЙНЫХ СИСТЕМ

ЭМАТИЧЕСКОГО УПРАВЛЕНИЯ ., - .

. Общий порядок синтеза нелинейных систем тот же, что и линей- ных (см. § 7-5 и 7-6). Особенности синтеза отдельных типов нели-нейных систем (дискретных и адаптивных) будут рассмотрены в-следующих частях книги.

Основным этапом синтеза по-прежнему является определение варьируемой части системы, сводящееся к выбору коррекции

исходя из заданных требований к качеству переходных процессов и точности при случайных воздействиях.

Как и для линейных САУ, при невысоких требованиях к качеству переходных процессов и точности в случайных режимах синтез осуществляется по условию обеспечения устойчивости с последующим выбором наилучших значений варьируемых параметров в пределах полученной области устойчивости в их пространстве.

Выбор коррекции по устойчивости осуществляется с помощью прямого метода Ляпунова, критерия абсолютной устойчивости В. М. Попова или путем определения гранцц области устойчивости методом гармонической линеаризации.

Синтез коррекции по требованиям к качеству переходных процессов выполняется с помощью критериев качества нелинейных САУ, изложенных в § 10-1. При этом, как и в случае линейных систем, большие удобства,! связанные с. графическим характером работы, дает синтез с помощью частотных характеристик и, в частности, логарифмических. В случае нелинейных САУ частотные характеристики могут быть использованы при синтезе на основе гармонической линеаризации и критерия В. М. Попова. В нервом случае синтез проводится с помощью частотных характеристик гармонически линеаризованной системы. Как говорилось, здесь в отличие от линейной САУ нелинейная система будет описана не одной, а серией частотных характеристик, являющихся функцией амплитуды А. Последнее отражает факт зависимости качества переходных процессов от величины отклонения X от установившегося значения и, соответственно, от величины вызвавшего это отклонение внешнего воздействия.

Если необходимо скорректировать степень этой зависимости, например, уменьшить ее, следует использовать нелинейную коррекцию, которая нужным образом изменит зависимость частотных характеристик от А.

При применении для синтеза с помощью частотных характеристик критерия В. М. Попова частотные характеристики варьируемой части системы выбираются так, чтобы выполнить требования, налагаемые при синтезе на устойчивость на характеристику WijVi) или при синтезе на заданное значением tj качество на характеристику Wn{- Ц + /<о).

Синтез в зтом случае также удобно проводить с помощью логарифмических характеристик [16].

Особенно эффективным методом синтеза нелинейных САУ является синтез с помощью вычислительных машин (см. § 7-5).

АСТЬ ТРЕТЬЯ

[ИСКРЕТНЫБ И ОПТИМАЛЬНЫЕ СИСТЕМЫ 1МАТИЧЕСК0Г0 УПРАВЛЕНИЯ

ГЛАВА ОДИННАДЦАТАЯ

РЕЛЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ

§ llVl. ПОНЯТИЕ о ДИСКРЕТНЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ и ИХ КЛАССИФИКАЦИЯ

Сигналы, действующие в системах автоматического унравления, бывают непрерывными и дискр е т ными. Соответственно этому все САУ делятся на системы ненрерыв-;НОго действия и системы дискретного действия.

В системах непрерывного действия (непрерывных системах) существуют то.чько непрерывные сигналы, являющиеся непрерывными функциями времени (рис. 11-1, о). Все звенья этих САУ- звенья непрерывного действия, т. е. их входные и выходные величины представляют собой непрерывные сигналы. ( САУ дискретного действия (дискретной САУ) называется сис-,тема, в которой хотя бы одна величина представляет собой дискретный сигнал. Дискретный сигнал изменяется во времени дискретно, скачками (рис. 11-1,6, в, г). Существуют дискретные САУ, в которых имеются только дискретные сигналы. Такие системы состоят полностью из звеньев дискретного действия, входные и выходные величины, которых являются дискретными. Однако в большинстве дискретных систем имеются как дискретные, так и непрерывные сигналы. В состав таких систем наряду со звеньями непрерывного и дискретного действия входят звенья, преобразующие непрерывные сигналы в дискретные, и звенья, осу-ществ.г[яющис обратное преобразование. Преобразование непрерывного сигнала в дискретный называйся квантованием сигнала. Существуют два основных вида квантования: по уровню (рис.11-1,б) и по времени (рис.11-1,в).

Сигнал, квантованный по уровню, может принимать только вполне определенные дискретные значения, соответствующие уровням, показанным нарис. 11-1, б, горизонтальными линиями. Сигнал квантованный по времени, изменяется скачком в фиксированные моменты времени, показанные на рис. 11-1, в вертикальными линиями.

Рис. 11-1. Непрерывные и дискретные сигналы.

На рис,-11-1, г изображен сигнал, квантованный и по уровню и по времени.

В соответствии с названными выше видами квантования САУ дискретного действия делятся на три типа: релейные, импульсные и цифровые. -Релейные САУ - зто системы с квантованием по уровню, импульсные - с квантованием по времени, а цифровые - с применением обоих видов квантования /

В настоящей главе рассмотрим релейные САУ. Импульсным и цифровым САУ будет посвящена следующая глава.

11-2. КЛАССИФИКАЦИЯ РЕЛЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Большинство релейных САУ можно представить, как показано на рис. 11-2. Здесь НП - непрерывная часть системы, & РЭ - релейный элемент. Релейный элемент осуществляет квантование непрерывного сигнала X по уровню, преобразуя его в дискрет-

Иногда [9; 22] под дискретными системами понимают только системы, в которых существует квантование по времени, т. е. импульсные и цифровые, а релейные системы выделяют в особый тип САУ. - -

Рис. 11-2. Релейная система автоматического управления.

сигнал У. Возможны и более сложные САУ, содержащие колько релейных элементов, разделенных частями непрерыв-го действия.

(Релейный элемент - это звено релейного действия, стати-характеристика которого может иметь вид одной из xapaj?-tCTHK, приведенных в пунктах .4,-5, 6 и7 яожения 5. Релейная характеристика может ,1ь й несимметричной. Релейным элементом системе может быть просто реле (электри-ское, пневматическое и т. п.), двигатель по-оянной скорости (управляемый только коман-,ли включен , выключен и, возможно, ребре без изменения величины скорости), какое- чувствительное звено релейного действия

Релейный элемент функционально может любым звеном управляющего устрой-хистемы - чувствительным, усилитель-вюЬолнительным - или входить в состав объекта управле-

кпичным примером релейной САУ являются широко распро-аенные релейные следящие системы с электрическим испол-шм двигателем. В этих системах усиление сигнала рассогласования и управление исполнительным двигателем осуществляются с помощью реле. К подобным системам относятся, в частности, исследованные в § 8-5 с помощью фазовой плоскости системы, изображенные на рис. 8-13 и 8-15.

Системы автоматического регулирования также очень часто выполняются релейными. На рис. 11-3 приведена схема релейной системы автоматического регулирования напряжения генератора постоянного тока с двухпозиционным реле. Напряжение генератора подается на электромагнитное реле Р, контакты эрого включают или выключают сопротивление R в цепи обмоткн-взбуждения генератора, изменяя тем самым ток возбуждения, а недовательно, и напряжевие генератрра. Установившийся режим Екботы системы - колебательный. Повышение напряжения генера-ора вызывает срабатывание реле и размыкание его нормально за-аутых контактов, благодаря чему происходит уменьшение тока эзбуждения и напряжения генератора. В результате реле вновь гцускает, опять замыкая свои нормально замкнутые контакты, алее п}>оцесс замыкания и размыкания контактов повторяется.

11-3. Двухпозиционная регулирования напря-ия генератора постоянного тока.