Передаточная функция Амплитудно-фазовая частотная функция

/со (О

(1-66)

(1-67)

т. е. амилитудно-фазовая характеристика, как показано на рис. 1-10, б, проходит по отрицательной мнимой полуоси.

201дк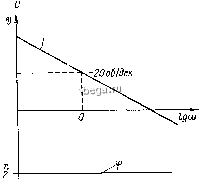

Рпс. 1-10. Характеристики идеального интегрирующего звена.

Согласно (1-67), .

(со) = 4;

ф(оз) = arctg

Л. а. X.

L(co) = 20 lg~= 201gA;-20lgco.

(1-68) (1-69)

Соответствующие амплитудная и фазовая характеристики изображены на рис. 1-10, в. Л. а. х. представляет собой прямую имеющую наклон к оси абсцисс -20 дб/дек. Ордината ее пои со = 1 (Ig со = 0) равна 20 Ig к.

Реальные интегрирующие звенья обычно обладают определенной инерционностью, вследствие чего их выход-

ная величина не равна точно интегралу от входной величины. Соответственно уравнение реального (инерционного) интегрирую- тего звена имеет вид:

. (Тр+1)ру = кх. (1-70)

Это уравнение второго порядка можно заменить следующей системой двух уравнений первого порядка:

pz = кх\

{Tp+i)y=z,

,дз 2 - новая промежуточная переменная.

Эта система соответствует последовательному соединению идеального интегрирующего звена и статического звена первого порядка. Таким образом, реальное интегрирующее звено не является элементарным типовым звеном, так как его можно представить в виде последовательного соединения уже известных нам типовых звеньев - идеального интегрирующего и статического первого порядка. I

Д. Идеальное дифс)еренцирующее звено

Уравнение этого звена

У = hpx,

(1-71)

т. е. в соответствии с нагганием выходная величина такого звена пропорциональна производной от входной величины. Коэффициент передачи дифференцирующего звена к имеет размерность сек. Переходная функция, согласно (1-71), равна

h{t) = kb{t). (1-72)

Передаточная функция

W{p) = kp. (1-73)

Амплитудно-фазовая частотная функция

PF (/со) = Д-со, (1-74)

т. е. амплитудно-фазовая характеристика дифференцирующего Звена, как показано на рис. 1-11, а, совпадает с положительной Мнимой полуосью. Согласно (1-74),

А{(и) = к{д; \

, . , (Ы\ я i (1-75)

9(co) = arctg-Q-J = 4-. I

Соответственно

L(co) = 20lg/c--20lgco. (1-76)

Амплитудная и фазовая характеристики звена приведены на рис. 1-11, бив.

Передаточная функция и соответственно характеристики дифференцирующего звена обратны передаточной функции и характеристикам интегрирующего звена.

Реальные дифференцирующие звенья обладают конечной инерционностью, вследствие чего осуществляемое ими дифференцирование не является точным. Уравнение реального дифференцирующего звена имеет вид:

(Тр-\-\)у=.крх. (1-77)

Его можно заменить системой уравнений:

Z = крх;

(Tp+i)y = z.

Поэтому, как и реальное интегрирующее звено,реальное дифференцирующее звено не является типовым, его можно заменить по-

1дш О

Рис. 1-11. Характеристики идеального дпфферешщрую-щсго звена.

следовательным соединением идеального дифференцирующего звена и статического звена первого порядка.

Е. Звено с постоянным запаздыванием

Это звено без искажения воспроизводит на выходе входную величину, как идеальное статическое звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:

jjx{t - T), (1.78)

причем у = О при г < т. Здесь т - время запаздывания.

Характеристики звена приведены на рис. 1-12, а и б. При этом, очевидно,

Л(о)) = 1; \ , ч } (1-79)

ф(С0) = -ТО). J

Поэтому амплитудно-фазовая частотная функция

М/(/о)) = е (1-80)

Соответственно передаточная функция

Ж(р) = е--р. (1-81)

Таким образом, с ирименением оператора р в символическом

luiU

Рис. 1-12. Характеристики звена с постоянным запаздыванием.

виде уравнение (1-78) звена с постоянным запаздыванием может быть представлено так:

у = е-Рх. (1-82)

Ж. Неустойчивые звенья

Рассмотренные выше звенья, кроме интегрирующего, устойчивые, так как все полюсы их передаточных функций имеют отрицательные действительные части. Они являются также, кроме звена с постоянным запаздыванием, и минимально-фазовыми, так как их передаточные функции не имеют еще и нулей с положительной действительной частью.

Примером неустойчивого звена является звено с передаточной функцией k

Тр - 1

которая отличается от передаточной функции статического звена первого порядка другим знаком перед единицей. Это звено мы уже рассматривали в предыдущем параграфе в качестве примера неминимально-фазового звена. Его переходная функция

h{t) = k[e- l),

весовая функция

а амплитудно-фазовая функция

(1-83) (1-84)

(1-85) 47

Соответствующие характеристики приведены на рис. 1-13, а, б, в.

Неустойчивыми являются также все звенья, передаточные функции которых отличаются от передаточных функций рассмотренных выше статических звеньев изменением знака любого из членов знаменателя на отрицательный. Примерами неустойчивых

Рис. 1-13. Характеристики неустойчивого звена первого порядка.

звеньев служат звенья со следующими передаточными функциями: к к к

-Тр + 1 Тр к

- Tip + Тр -f 1

Tip-T.p + i Tip + T,p-i-

Физический смысл термина неустойчивость в самом общем виде был раскрыт во введении и детально будет рассмотрен в четвертой главе. Пока же отметим только, что переходные характеристики неустойчивых звеньев неограниченно растут со временем. Кроме того, напомним, что все неустойчивые звенья являются и неминимально-фазовыми.

§ 1-5. ПОЛУЧЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ЧАСТОТНЫХ ХАРАКТЕРИСТИК СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НО ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ И ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ ЕЕ ЗВЕНЬЕВ

В результате разбиения САУ на звенья нанравленного действия и получения математи ческого описания звеньев в виде передаточных функций, частотных или переходных характеристик составля-

ется структурная схема системы. По структурной схеме можно затем получить передаточную функцию или характеристики системы в целом. Рассмотрим этот последний этап математического описания САУ.

А. Получение передаточной функции системы по передаточным функциям звеньев

Если имеются уравнения всех звеньев системы, то описанием последней является система этих уравнений. Исключив из нее обычным порядком промежуточные переменные, можно получить одно дифференциальное уравнение высокого порядка, связываю-

W,(p)

Wn(P>

Рис. 1-14. Соединения звеньев.

щее выходную величину системы с определенной входной величиной- каким-либо возмущением или задающим воздействием. Однако значительно более просто можно получить описание системы, если оперировать передаточными функциями звеньев. Начнем с простейших случаев.

Передаточная функция цепочки последовательно соединенных Л звеньев направленного действия (рис. 1-14, а). В этом случае 1 имеем систему уравнений:

У==п iP) Уп-V

Исключив отсюда промежуточные переменные, получим y[W,{p)W,{p) ...W,{p)\xW{p)x.