Рйс. 3.37. Направленный граф относительных приращений параметров трехфазного емкостно-полу-проводникового ПРА

ЧТО обеспечивает эффективную работу полупроводникового стабилизатора тока. Однако если неравенство (3.96) выполняется при С/ф ; , Сф , , и то в номинальном режиме оно имеет больший запас. Это приводит к большим потерям мощности в полупроводниковом стабилизаторе тока и к снижению КПД трехфазного аппарата.

Для повышения КПД в схему можно добавить три добавочных цепи, обеспечивающие управление стабилизатором тока таким образом, чтобы (3.96) при всех колебаниях параметров выполнялось с минимальным запасом. На рис. 3.37 эти добавочные связи показаны пунктиром. Из условия А[,,с = 0 находим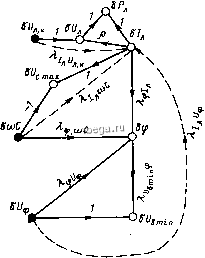

(3.97)

Эта связь может реализоваться при первоначальной настройке ПРА. Из условия \fj ,fj =1 получаем

(3.98)

Эта настройка может осуществляться при смене лампы. При непрерывной настройке она должна быть между узлами 5С/д и 5/, что, вообще говоря, более правильно. Однако при малых значениях коэффициента, характеризующего наклон статической характеристики, рО обе эти связи эквивалентны.

И, наконец, из условия u, i u = получим

(3.99)

Глава четвертая

РАСЧЕТ СХЕМ ПРА С ИСПОЛЬЗОВАНИЕМ ПРИНЦИПА

ДИФФЕРЕНЦИАЛЬНОЙ АППРОКСИМАЦИИ ЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ РАЗРЯДНЫХ ЛАМП

4.1. АНАЛИЗ СХЕМ ПРА, РАБОТАЮЩИХ НА ПРОМЫШЛЕННОЙ

ЧАСТОТЕ

Принцип расчета схем ПРА с использованием дифференциальных моделей применяется при расчете таких схем, для которых необходимо провести расчеты при широкой вариации режимов работы, а формы напряжения и тока лампы в этих режимах не могут быть предсказаны заранее.

Рассмотренные в гл. 1 и 3 методы расчета, основанные на алгебраической аппроксимации характеристик разрядных ламп, достаточно сложны в применении даже к простейшим схемам и не пригодны для расчета целого ряда более сложных импульсных полупроводниковых и комбинированных схем ПРА. Связано это с тем, что при высоких скоростях изменения тока лампы 1д/Л>10А/с в силу инерционности разряда напряжение на лампе Мд(?) начинает сильно зависеть от формы тока /д(?), и простейшие алгебраические аппроксимации формы напряжения u {t) становятся непригодными.

От этих недостатков свободны математические модели электрических параметров разрядных ламп, основанные на дифференциальной аппроксимации процессов, происходяпщх в плазме столба разряда, практически пригодные для расчетов всех групп схем. В § 2.3 показано, что при формировании уравнений для цепей, содержащих разрядные лампы, последние должны заменяться резистивными двухполюсниками с инерционными параметрами. Система полученных уравнений решается при определенных значениях начальных условий (напряжении на конденсаторах, токе дросселей, проводимости ламп). Для нахождения установившегося режима вычисления производятся либо последовательным приближением к окончанию переходного процесса, либо методом пристрелки, т. е. подбором Начальных условий, обеспечивающих попадание в установившийся режим.

Такими методами можно рассчитывать цепи, обладающие абсолютной устойчивостью, когда установившийся режим не зависит от выбранных начальных условий. Если такой уверенности нет, цепь предварительно должна быть проверена на устойчивость.

Вопросы устойчивости электрических цепей с дугой подробно рассмотрены О.Я.Новиковым и его учениками [4.1] с использоваием широкого класса аппроксимирующих уравнений.

Вопросы устойчивости /?CL-ueneii с дугой исследованы в [4.2] при аппроксимации характеристик дуги уравнением Майра [4.2]. В [4.3] исследование устойчивости дуги проведено на аналоговой вычислительной машине, критерии устойчивости получены при учете средней за полупериод проводимости дуги. При этом сопротивление дуги в момент перехода тока через нуль скачком изменялось до нового постоянного значения.

Анализ устойчивости импульсных схем с разрядными лампами проведен в [4.4 с использованием аппроксимирующего уравнения Френсиса. Показано, что проверка на устойчивость в малом может осуществляться по критериям Найквиста, Михайлова, Ляпунова и т. д. Проверку устойчивости в большом целесообразно проводить по критерию Ляпунова.

Расчеты электрических цепей с дугой отражены в работах И. С. Таева, Ю. С. Свирчука [1.18], О. Я. Новикова [4. ] и др.

Расчеты индуктивных ПРА с лампами типа ДРЛ и комбинированных ПРА с дросселем и полупроводниковым переключателем выполнены в [1.19, 4.4] с использованием предложенного их авторами дифференциального уравнения первой-степени с постоянными коэффициентами. Е. Пик и А. Спенсер провели расчеты индуктивного и емкостного ПРА с люминесцентной лампой, параметры которой аппроксимировались уточненным уравнением Френсиса. Д. Энгель на основе уравнения Френсиса выполнил расчет импульсного полупроводникового ПРА. И, наконец, в [4.4] проведен расчет схемы комбинированного ПРА на основе предложенной математической модели параметров разрядных ламп.

Такое незначительное количество публикаций по методам расчета, основанным на дифференциальной аппроксимации параметров разрядных ламп, объясняется в основном двумя причинами. Во-первых, до настоящего времени отсутствовали подходящие дифференциальные аппроксимации, с достаточной точностью описывающие динамические характеристики массовых разрядных ламп (люминесцентных ламп, типов ДРЛ и ДРИ, натриевых ламп высокого давления), во-вторых, интерес к этим методам возник сравнительно недавно, при появлении полупроводниковых ПРА, которые не могут быть рассчитаны другими методами.

В настоящей главе осуществлен анализ основных групп ПРА с использованием дифференциальных моделей, что достаточно полно иллюстрирует возможности этого метода.

Электромагнитные, резистивные и полупроводниковые ПРА, работающие на промышленной частоте, можно успешно рассчитывать традиционными методами на основе алгебраической аппроксимации ВАХ разрядных ламп. Ниже приводится расчет схем таких ПРА с применением разработанных мате!у1атических

моделей электрических параметров ламп. Расчеты позволяют оценить точность метода и иллюстрируют его возможности.

Схема стартерного индуктивно-емкостного ПРА показана на рис. 3.12. При нелинейных элементах схемы (дроссель, резистор, конденсатор) уравнения электрического состояния имеют вид

dJdt =u {t)-Uc{Qc)-F, (Ч,); dQcldt = i {,), (4.1)

где Fl - нелинейная функция от / ; *F:

Если в схеме применены линейные элементы, то /? = const, L = const; С=const; 4 = L4; Q = CUc.

Система (4.1) применима для расчета как индуктивно-емкостного, так и индуктивного ПРА. В последнем случае

Для анализа емкостного ПРА с полупроводниковым стабилизатором тока (см. рис. 3.29) система (4.1) должна быть заменена уравнением

dQc/dt = F2 (Q [u {t)-Uc{Qc)l (4.2)

где F2 - нелинейная функция от

F2(Q = GJ[G R {Q+ll (4.3)

где RJij) - сопротивление нелинейного стабилизатора тока (см. рис. 3.30).

При емкостном балласте с линейным резистором R (4.2) принимает вид

dQc/dtG [u {t)-Qc/C]/(l+G,R). (4.4)

И, наконец, при резистивном нелинейном балласте система (4.1) переходит в одно алгебраическое уравнение

R{in)in + UG. = u {t).

(4.5)

Уравнения (4.1) и (4.5) решают совместно с (2.10) и (2.16). Численное интегрирование уравнений осуществляют на ЭВМ. Расчеты показали следующее [4.5]:

1) установившийся режим для всех типов балластов не зависит от принятых начальных условий;

2) длительность переходного режима для всех типов балластов существенно зависит от принятых начальных условий;

3) самый короткий переходный режим наблюдается при работе люминесцентной лампы с линейным или нелинейным резистивным балластом. Его длительность в самом неблагоприятном случае не превосходит двух периодов. Наиболее длительный переходный режим имеет место в схеме с индуктивно-емкостным балластом и может достигать 7 - 8 периодов;

4) нелинейность характеристики дросселя оказывает существенное влияние на все параметры разрядной лампы. При увеличении нелинейности ухудшается форма тока лампы, уменьшается коэффициент мощности лампы, понижается стабильность ее работы, что особенно, сказывается в схеме с индуктивным балластом;

5) соотношение реактивных составляющих балластов х/х существенно влияет на форму тока лампы. При Хс/х>4,6 в токе лампы появляются паузы. Расчет критических соотношений {и /и )р, при которых осуществляется переход к режиму горения с паузами тока, показал хорошее совпадение с расчетами, проведенными на базе алгебраической аппроксимации (см. рис. 3.15);

6) в индуктивных и индуктивно-емкостных ПРА в режимах без паузы тока действующее значение напряжения на лампе U несколько выше установившегося напряжения на постоянном токе Uq. Для люминесцентных ламп f/ 1,02 ч-1,025) C/q, ламп типа ДРЛ f/ (l,03H-1,035) f/o, что хорошо согласуется с экспериментом;

7) использование уточненной модели люминесцентной лампы, учитывающей зависимость напряжения Uq от приведенной проводимости gj повышает точность расчетов неноминальных режимов, когда напряжение Uq заметно отличается от номинального С/о ом- При расчете номинальных режимов уточненная модель [см. (2.10а и 2.106)] и нелинейная модель первого порядка [сМ. (2.10а - 2.10в)] дают практически одинаковые результаты (расхождение менее 1%);

8) использование уточненных моделей ламп типа ДРЛ [см. (2.16)] несколько повышает точность расчета перечисленных выше схем. Повышение точности незначительно при расчете режимов без пауз тока, в режимах с паузой тока отмечено снижение погрешности на 1 -1,5%;

9) точность всех расчетов высокая. При расчете режимов без пауз тока и при линейной характеристике балласта погрешности расчета мощности и тока лампы и напряжения на балласте не превышали +2%. Расчеты при нелинейной характеристике балласта дали погрешность около 5%, что, по-видимому, связано с недостаточной точностью аппроксимации нелинейной характеристики, ее отличием от реальной характеристики дросселя, использованного в эксперименте. Расчеты полупроводниковых и резистивных схем показали отклонение от экспериментальных результатов в пределах +4%.

Сравнение некоторых расчетных и экспериментальных результатов приведено в табл. 4.1. При расчете линейных схем ПРА, обеспечивающих работу лампы в режиме без пауз тока, погрешность расчетов не превышает 2%. При нелинейном дросселе погрешность увеличивается до 4,5% и наибольшая

Таблица 4.1. Сравнение результатов расчета н эксперимента схем ПРА иа

нромышленвон частоте

Тип лампы

Люминесцентная

Люминесцентная*

Люминесцентная

Люминесцентная

Люминесцентная

ДРЛ 125

ДРЛ80

Тип; параметры ПРА

Линейный индуктивный; L=\,24 Гн, R = = 38,6 Ом, [/ = 220 В

Линейный индуктивный; L=l,28 Гн, R = = 206 Ом, [/ =146 В

Нелинейный индуктивный; Lo= 1,45 Гн, R=4l Ом, [/ = 220 В

Линейный индуктивно-емкостный; L = = 1,24Гн, С=3,73 мкф, Л = 38,6 Ом, [/ = 220 В

Емкостный полупроводниковый; [/ = = 220 В, С=6,8 мкф

Линейный индуктивный; L=0,425rH, Л = = 10,0 Ом, [/ = 220 В

Лилейный резистив-ный; Л =165 Ом, [/=220 В

Параметр лампы, еди ницы измерения

/л, А Р., Вт

/л, А Л, Вт

4, А /л.. А Л, Вт

/л, А

4, А 4 , А

-Рл, Вт

ant!

Р., Вт

4, А / А Р., Вт

Значение параметра

расчетное

0,437 0,632 40,2

0,116 0,190 10,2

0,450 0,758 40,1

0,440 0,705 42,4

0,440 0,510 21,5

1,140 1,670 126,5

0,692 1,080 62,5

экспериментальное

0,430 0,635 39,7

0,110 0,180 9,8

0,435 0,730 39,0

0,435 0,700 41,9

0,428 0,500 20,8

1,150 1,700 125,0

0,670 1,050 64,5

* Неноминальный режим с паузами тока.

погрешность 5,5% достигается при расчете линейной индуктивной схемы, в которой лампа работает в резко неноминальном режиме и с большой паузой тока.

В режимах без пауз тока форма напряжения на лампе приближается к прямоугольной (см. рис. 2,5,а, б), поэтому большая часть расчета производится при практически постоянном значении функции (mJ. В режимах с паузами тока напряжение на лампе изменяется в широких пределах (см. рис. 2.7 и 4.1) и на точность расчетов влияет значение функции