После подстановки в эту формулу выходящего из полюса магнитного потока, равного

получим

Vo

0,8 В, Dp D - b,n

(22)

Правомерность сделанных предположений обосновывается следующими соображениями.

1. На рис. 60 построена известным графическим методом картина плоско-параллельного магнитного поля под полюсом при условии постоянства удельной магнитной проницаемости стали. Можно заметить, что основная доля магнитного потока сосредоточена в верхней части сечения. Если учесть цилиндрич-ность ротора, аналогично тому как это было сделано при анализе растекания в нем тока (см. раздел IV, рис. 54), то силовые трубки из-за значительно возросшего магнитного сопротивления в центральной части ротора, еще более окажутся смещенными * к его наружной поверхности. Одновременно будет происходить выравнивание индукции в рассматриваемой зоне.

Описанное смещение трубок из центра ротора будет несколько снижено уменьшением удельной магнитной проницаемости по мере удаления от оси ротора из-за роста напряженности поля, как это следует из выражения (!5).

2. На рис. 6! показана зависимость величины Кп от отноше-

ния Из графика следует, что при отношении

* При построении поля не учитывалось центральное отверстие ротора Оно также способствует концентрации потока около поверхности ротора.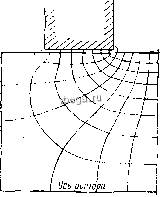

Рис. 60. Картина магнитного поля

Рис. 61

грешность в задании Вг не может дать существенного отклонения величины Кн, а следовательно, и Fp.

Таким образом, можно в первом приближении Ка принимать постоянной величиной. В этом случае выражение (19) удобно представить в виде

R-dl,

где величина

(23)

(24)

представляет собой максимальную напряженность поля в роторе от тока обмотки возбуждения.

Перейдем к определению fp для принятой расчетной схемы (см. рис. 59). Для зоны ротора под полюсом имеем

/? = /?p-rslnP,

откуда по (23) найдем

f (/?2-rsinP) rfifp.

В результате для заданной радиусом г линии определим

(25)

Для зоны ротора, заключенной между полюсом и контактом токосъема, имеем

р 11 гт

ГПК

r)-dl,

(26)

откуда для линии, заданной радиусом г, получим

Суммируя (25) и (26), окончательно найдем намагничивающую силу на полюс, которая необходима для проведения через сталь ротора рабочего магнитного потока при заданных значениях тока и средней индукции в зазоре

(27)

Множитель, стоящий перед Нтг, представляет собо.эквива-лентные длины 1э расчетных силовых линий, положение которых .определяется параметром г. ,-, .

На рис. 62 показана зависимость 1о от отношения -7~, где

От - ширина кольцевого полюса.

При расчете были приняты следующие размеры униполярного генератора (при 150 ка, 67 в, 3000 об/мин): р=0,4 м; 1тк=-0,\2м; Ьга = 0Л9м.

В некотором масштабе представленная кривая также характеризует изменение намагничивающей силы по расчетным силовым линиям. Расчет показал, что среднеарифметическая величина эквивалентной длины (/эо=0,21 м) близка к длине, определенной приг=0,56т (/эо = 0,22 i).

ил СИ

ЮО 11.05

П а,2 4 0.6 Рис. 62

Таким образом, для определения средней величины Fpo можно ре-ком ендов а ть вычисление по (27) цри г=0,5 Ьт.

Представляет интерес оценка величины Fpo по сравнению с намагничивающей силой, необходимой для проведения магнитного потока полюса через воздушные зазоры под парой полюсов. При следующих указанных данных: Вг=1,7 тл; Вн = 2,2 тл согласно рис. 61 находим, что /(п=1,05. Если радиус ротора /?р = 0,4 м и ток нагрузки /=150-10 а, то согласно (24) найдем, что Яу, = ,59,8 10 aJM и Ягт = 62,8 10 о/ж. Используя ранее полученное значение /эо = 0,22 i, определим, что fp = = 13,8 103 д суммарном воздушном зазоре под двумя полюсами 26 = 0,01 м и fioo =1,7 тл необходима намагничивающая сила, равная Л = 13,5 10 а.

Таким образом, величины намагничивающих сил на сталь ротора и пару воздушных зазоров под полюсами для принятых данных оказались однопорядковыми величинами.

В связи с относительно большой величиной намагничивающей силы на сталь ротора и ее непостоянством для разныхрас-

четных силовых линии распределение индукции в воздушном зазоре под средними* полюсами будет также неравномерным.

Вид кривой на рис. 62 показывает, что наибольшая индукция будет под краем полюса со стороны токосъема. Не представляет сложности рассчитать соответствующую кривую распределения индукции в зазоре машины под средними полюсами.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ РАССЕЯНИЯ ОБМОТКИ ВОЗБУЖДЕНИЯ

Магнитная цепь статора может быть разделена на следующие три характерных участка, через которые проходит основной магнитный поток: спинка статора, сердечник полюса и зона полюсного башмака. Для обеспечения точности при расчете намагничивающих сил первых двух участков необходимо учитывать коэффициент рассеяния полюсов, который для униполярных машин достигает существенной величины. В связи с этим получим формулы для его определения.

Аналитическое решение поставленной задачи значительно упрощается, если картину поля рассеяния в полюсном окне рассматривать как плоскую, т. е. пренебречь кривизной катушки возбуждения. Точность полученных при этом выражений будет тем выше, чем меньше отношение высоты катушки возбужде-

НИЯ к ее среднему радиусу . В современных крупных униполярных машинах с непосредственным охлаждением водой катушек возбуждения указанное отношение относительно мало. Например, для приведенного в разделе VII расчета униполярного генератора оно составило всего 0,24.

Коэффициент рассеяния полюсного сердечника представляет собой величину

,(28)

где Ф - рабочий магнитный поток; Ф - поток рассеяния.

Рассматривая межполюсное окно как прямоугольный паз электрической машины с проводимостью на единицу длины к, получим

* Так как в зоне крайних полюсов сталь ротора насыщена относительно слабо, то будет иметь место выравнивание индукции под указанными по- люсамн

fio Ь (£ р-f ft ) fe

(29)

где fe-намагничивающая сила обмотки возбуждения на пару полюсов; Лп - высота полюсного окна.

Если принять, что силовые линии потока рассеяния между стенками и полюсом являются прямыми линиями, то, как известно,

где Ьд - ширина полюсного окна.

Точное выражение для линейной проводимости паза, учитывающее действительную картину магнитного поля рассеяния, имеет вид [30]

- Щ- arctg -f . (30)

к 2 Un

Оно обеспечивает хорошую точность, как это будет показано в разделе V, при условии

Для униполярных генераторов отношение имеет второй порядок малости, поэтому (30) значительно упрощается

(31)

Здесь уместно привести выражение для расчета коэфициен-та рассеяния (по потокоснеплению) обмотки возбуждения, так как вывод ее аналогичен коэффициенту рассеяния полюсов.

Действительно

- 1 +

Торф

= I +

прячем

4 = ir- +

Лп - fie

(32)

К - he

-0.221,

> 1.

/ге - высота катушки возбуждения.

V. ПОТЕРИ В УНИПОЛЯРНЫХ МАШИНАХ

Успешное освоение жидкометаллического контакта позволило в современных униполярных машинах снизить до минимума величину активных потерь; так, для мощных генераторов они составляют всего 2-4%. Однако, несмотря на относительно малые потери, анализ их величины и распределения в машине при проектировании чрезвычайно важен, поскольку от результатов анализа зависит точность теплового расчета машины и выбора оптимальных размеров активной зоны токосъемных устройств.

Потери в униполярной машине целесообразно разделить на две однородные группы: механические и электрические.

К первой группе следует отнести потери трения в жидкометаллической среде токосъемных устройств, в подшипниках и уплотнениях, вентиляционные; ко второй - потери, вызванные протеканием электрического тока в теле ротора, медных токо-ведущих частях, жидкометаллической среде и переходных соединительных контактах.

Наибольшие трудности вызывает расчет потерь трения в жидкометаллической среде токосъемных устройств, поэтому ниже ему уделяется большое внимание.

ПОТЕРИ ТРЕНИЯ В ЖИДКОЙ СРЕДЕ ТОКОСЪЕМНОГО УСТРОЙСТВА

КОЛЬЦЕВОГО ТИПА

Потери механического трения в токосъемных устройствах, как правило, составляют существенную долю общих потерь машины. Например, для современного униполярного генератора на скорость вращения 3000 об/мин и ток 150 ка (расчет приведен в разделе VII) это соотношение составило 24%. В связи с этим желательна повышенная точность их расчета и обоснованный выбор геометрических размеров контактной зоны, от которых в значительной мере зависят эти потери. В работе Ю. Ю. Каунаса [16] дано аналитическое решение задачи определения механических потерь в жидкости, заключенной между поверхностями вращающихся соосных цилиндров. Проведенные им экспериментальные исследования с ртутью, а также сопоставления результатов расчета ряда гидродинамических систем с ранее известными опытными данными других авторов дали хорошие результаты.

Предварительно кратко рассмотрим некоторые положения гидродинамики, необходимые для изложения основного материала.

Принято различать два типа движения жидкости: ламинарное, когда слои жидкости как бы скользят относительно друг друга, и турбулентное, когда ее частицы движутся хаотично. Тот или иной характер движения зависит от некоторой безраз- мерной величины, которая получила название числа Рейнольд-